本篇文章主要用图片的形式讲解了堆排序流程,之后用Java代码实现堆排序并且分析时间复杂度,具有一定参考价值,感兴趣的朋友可以了解一下。
一、引言二、图解堆排序(heapsort)三、java代码实现及时间复杂度分析四、总结
一、引言
优先队列可以用于以O(NlogN)时间排序,正如上一篇的求解topK问题中用到的思想一样,这种思想就是堆排序(heapsort)。
二、图解堆排序(heapsort)
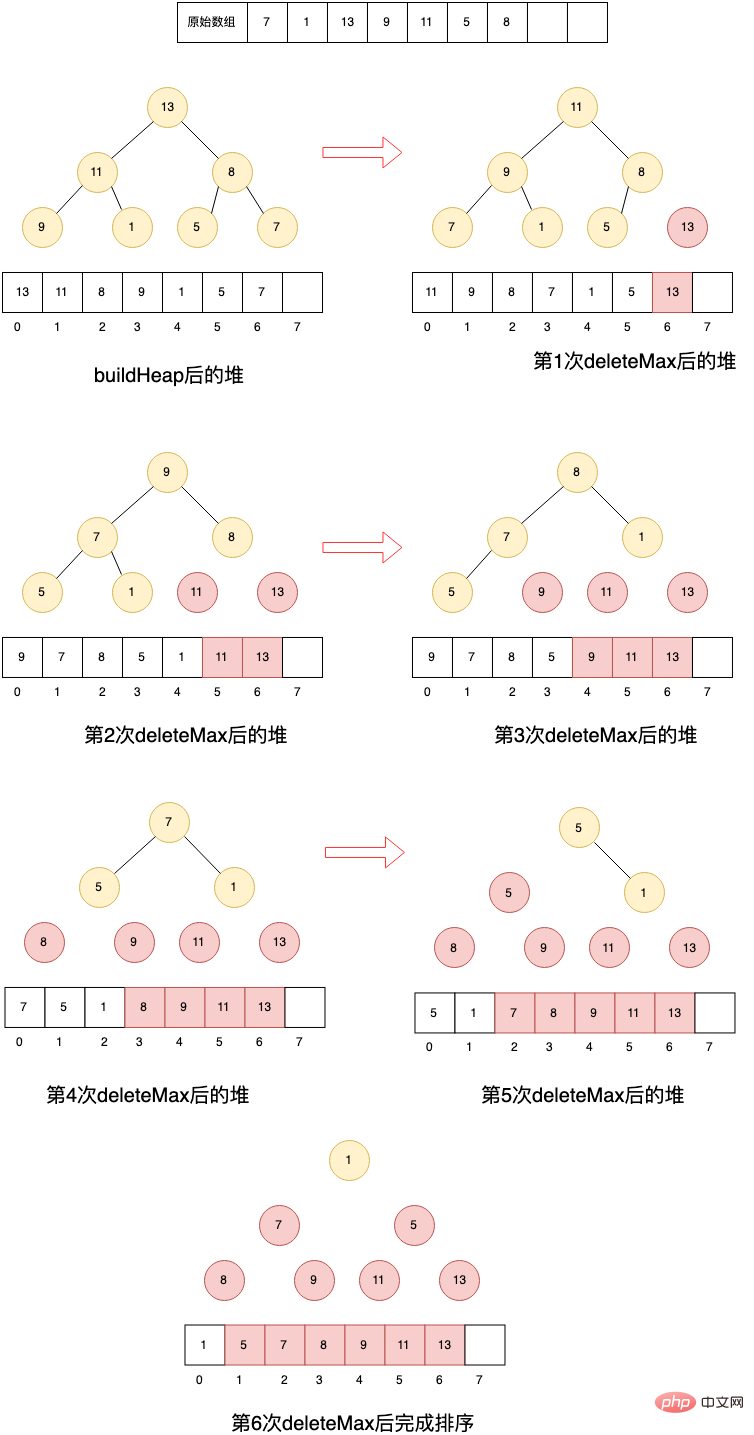
- 算法思想:通过将数组元素进行buildHeap进行堆序化(构建大顶堆);再对堆进行N-1次deleteMax操作。这里有个技巧,如果使用新的数组来存储,需要O(N)的空间;但每次deleteMax会空出一个位置,并将尾端的节点进行下滤操作,那我们就可以将deleteMax的数据放到尾端。
- 堆排序过程:
对二叉堆不了解的可以看看图解优先队列(堆)
三、java代码实现及时间复杂度分析
我们从数组下标0开始,不像二叉堆从数组下标1开始。
代码实现
public class Heapsort { public static void main(String[] args) { Integer[] integers = {7, 1, 13, 9, 11, 5, 8}; System.out.println("原序列:" + Arrays.toString(integers)); heapsort(integers); System.out.println("排序后:" + Arrays.toString(integers)); } public static <T extends Comparable<? super T>> void heapsort(T[] a) { if (null == a || a.length == 0) { throw new RuntimeException("数组为null或长度为0"); } //构建堆 for (int i = a.length / 2 - 1; i >= 0; i--) { percDown(a, i, a.length); } //deleteMax for (int i = a.length - 1; i > 0; i--) { swapReferences(a, 0, i); percDown(a, 0, i); } } /** * 下滤的方法 * * @param a:待排序数组 * @param i:从哪个索引开始下滤 * @param n :二叉堆的逻辑大小 * @param <T> */ private static <T extends Comparable<? super T>> void percDown(T[] a, int i, int n) { int child; T tmp; for (tmp = a[i]; leftChild(i) < n; i = child) { child = leftChild(i); if (child != n - 1 && a[child].compareTo(a[child + 1]) < 0) { child++; } if (tmp.compareTo(a[child]) < 0) { a[i] = a[child]; } else { break; } } a[i] = tmp; } private static int leftChild(int i) { return 2 * i + 1; } /** * 交换数组中两个位置的元素 * * @param a:目标数组 * @param index1 :第一个元素下标 * @param index2 :第二个元素下标 * @param <T> */ private static <T> void swapReferences(T[] a, int index1, int index2) { T tmp = a[index1]; a[index1] = a[index2]; a[index2] = tmp; }}//输出结果//原序列:[7, 1, 13, 9, 11, 5, 8]//排序后:[1, 5, 7, 8, 9, 11, 13]时间复杂度:buildHeap使用O(N)的时间,元素下滤需要O(logN),需要下滤N-1次,所以总共需要O(N+(N-1)logN) = O(NlogN)。从过程可以看出,堆排序,不管最好,最坏时间复杂度都稳定在O(NlogN)。
空间复杂度:使用自身存储,无疑是O(1)。
四、总结
本篇通过画图,说明堆排序的过程,清晰明了知道堆排序先经过堆序化,再通过deleteMax进行排序。其空间复杂度是O(1),时间复杂度稳定在O(NlogN)。
以上就是Java学习之堆排序流程图解以及代码讲解的知识。速戳>>知识兔学习精品课!
