冒泡排序
冒泡排序(英语:Bubble Sort)是一种简单的排序算法。它重复地走访过要排序的数列,一次比较两个元素,如果他们的顺序(如从大到小、首字母从A到Z)错误就把他们交换过来。
过程演示:

实例
#include <stdio.h>void bubble_sort(int arr[], int len) { int i, j, temp; for (i = 0; i < len - 1; i++) for (j = 0; j < len - 1 - i; j++) if (arr[j] > arr[j + 1]) { temp = arr[j]; arr[j] = arr[j + 1]; arr[j + 1] = temp; }}int main() { int arr[] = { 22, 34, 3, 32, 82, 55, 89, 50, 37, 5, 64, 35, 9, 70 }; int len = (int) sizeof(arr) / sizeof(*arr); bubble_sort(arr, len); int i; for (i = 0; i < len; i++) printf("%d ", arr[i]); return 0;}
选择排序
选择排序(Selection sort)是一种简单直观的排序算法。它的工作原理如下。首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
过程演示:


实例
void selection_sort(int a[], int len) { int i,j,temp; for (i = 0 ; i < len - 1 ; i++) { int min = i; // 记录最小值,第一个元素默认最小 for (j = i + 1; j < len; j++) // 访问未排序的元素 { if (a[j] < a[min]) // 找到目前最小值 { min = j; // 记录最小值 } } if(min != i) { temp=a[min]; // 交换两个变量 a[min]=a[i]; a[i]=temp; } /* swap(&a[min], &a[i]); */ // 使用自定义函数交換 }} /*void swap(int *a,int *b) // 交换两个变量{ int temp = *a; *a = *b; *b = temp;}*/
插入排序
插入排序(英语:Insertion Sort)是一种简单直观的排序算法。它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。插入排序在实现上,通常采用in-place排序(即只需用到 {\displaystyle O(1)} {\displaystyle O(1)}的额外空间的排序),因而在从后向前扫描过程中,需要反复把已排序元素逐步向后
挪位,为最新元素提供插入空间。过程演示:

实例
void insertion_sort(int arr[], int len){ int i,j,temp; for (i=1;i<len;i++){ temp = arr[i]; for (j=i;j>0 && arr[j-1]>temp;j--) arr[j] = arr[j-1]; arr[j] = temp; }}
希尔排序
希尔排序,也称递减增量排序算法,是插入排序的一种更高效的改进版本。希尔排序是非稳定排序算法。
希尔排序是基于插入排序的以下两点性质而提出改进方法的:
- 插入排序在对几乎已经排好序的数据操作时,效率高,即可以达到线性排序的效率
- 但插入排序一般来说是低效的,因为插入排序每次只能将数据移动一位
过程演示:

实例
void shell_sort(int arr[], int len) { int gap, i, j; int temp; for (gap = len >> 1; gap > 0; gap = gap >> 1) for (i = gap; i < len; i++) { temp = arr[i]; for (j = i - gap; j >= 0 && arr[j] > temp; j -= gap) arr[j + gap] = arr[j]; arr[j + gap] = temp; }}
归并排序
把数据分为两段,从两段中逐个选最小的元素移入新数据段的末尾。
可从上到下或从下到上进行。
过程演示:

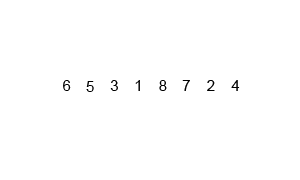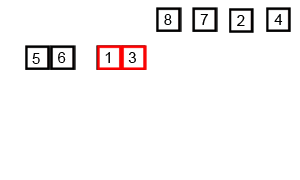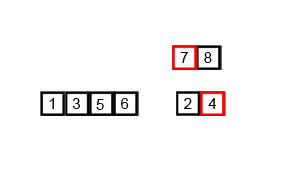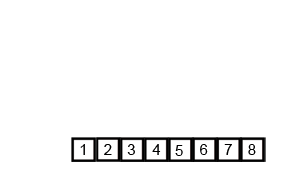
迭代法
int min(int x, int y) { return x < y ? x : y;}void merge_sort(int arr[], int len) { int* a = arr; int* b = (int*) malloc(len * sizeof(int)); int seg, start; for (seg = 1; seg < len; seg += seg) { for (start = 0; start < len; start += seg + seg) { int low = start, mid = min(start + seg, len), high = min(start + seg + seg, len); int k = low; int start1 = low, end1 = mid; int start2 = mid, end2 = high; while (start1 < end1 && start2 < end2) b[k++] = a[start1] < a[start2] ? a[start1++] : a[start2++]; while (start1 < end1) b[k++] = a[start1++]; while (start2 < end2) b[k++] = a[start2++]; } int* temp = a; a = b; b = temp; } if (a != arr) { int i; for (i = 0; i < len; i++) b[i] = a[i]; b = a; } free(b);}
递归法
void merge_sort_recursive(int arr[], int reg[], int start, int end) { if (start >= end) return; int len = end - start, mid = (len >> 1) + start; int start1 = start, end1 = mid; int start2 = mid + 1, end2 = end; merge_sort_recursive(arr, reg, start1, end1); merge_sort_recursive(arr, reg, start2, end2); int k = start; while (start1 <= end1 && start2 <= end2) reg[k++] = arr[start1] < arr[start2] ? arr[start1++] : arr[start2++]; while (start1 <= end1) reg[k++] = arr[start1++]; while (start2 <= end2) reg[k++] = arr[start2++]; for (k = start; k <= end; k++) arr[k] = reg[k];}void merge_sort(int arr[], const int len) { int reg[len]; merge_sort_recursive(arr, reg, 0, len - 1);}
快速排序
在区间中随机挑选一个元素作基准,将小于基准的元素放在基准之前,大于基准的元素放在基准之后,再分别对小数区与大数区进行排序。
过程演示:

迭代法
typedef struct _Range { int start, end;} Range;Range new_Range(int s, int e) { Range r; r.start = s; r.end = e; return r;}void swap(int *x, int *y) { int t = *x; *x = *y; *y = t;}void quick_sort(int arr[], const int len) { if (len <= 0) return; // 避免len等於負值時引發段錯誤(Segment Fault) // r[]模擬列表,p為數量,r[p++]為push,r[--p]為pop且取得元素 Range r[len]; int p = 0; r[p++] = new_Range(0, len - 1); while (p) { Range range = r[--p]; if (range.start >= range.end) continue; int mid = arr[(range.start + range.end) / 2]; // 選取中間點為基準點 int left = range.start, right = range.end; do { while (arr[left] < mid) ++left; // 檢測基準點左側是否符合要求 while (arr[right] > mid) --right; //檢測基準點右側是否符合要求 if (left <= right) { swap(&arr[left],&arr[right]); left++;right--; // 移動指針以繼續 } } while (left <= right); if (range.start < right) r[p++] = new_Range(range.start, right); if (range.end > left) r[p++] = new_Range(left, range.end); }}
递归法
void swap(int *x, int *y) { int t = *x; *x = *y; *y = t;}void quick_sort_recursive(int arr[], int start, int end) { if (start >= end) return; int mid = arr[end]; int left = start, right = end - 1; while (left < right) { while (arr[left] < mid && left < right) left++; while (arr[right] >= mid && left < right) right--; swap(&arr[left], &arr[right]); } if (arr[left] >= arr[end]) swap(&arr[left], &arr[end]); else left++; if (left) quick_sort_recursive(arr, start, left - 1); quick_sort_recursive(arr, left + 1, end);}void quick_sort(int arr[], int len) { quick_sort_recursive(arr, 0, len - 1);}
