在统计学中,线性回归(Linear Regression)是利用称为线性回归方程的最小平方函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。
简单对来说就是用来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。
回归分析中,只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量,且因变量和自变量之间是线性关系,则称为多元线性回归分析。
一元线性回归分析法的数学方程:
y = ax + b
y 是因变量的值。
x 是自变量的值。
a 与 b 为一元线性回归方程的参数。
接下来我们可以创建一个人体身高与体重的预测模型:
- 1、收集样本数据:身高与体重。
- 2、使用 lm() 函数来创建一个关系模型。
- 3、从创建的模型中找到系数,并创建数学方程式。
- 4、获取关系模型的概要,了解平均误差即残差(估计值与真实值之差)。
- 5、使用 predict() 函数来预测人的体重。
准备数据
以下是人的身高与体重数据:
# 身高,单位 cm151, 174, 138, 186, 128, 136, 179, 163, 152, 131# 体重,单位 kg63, 81, 56, 91, 47, 57, 76, 72, 62, 48
lm() 函数
在 R 中,你可以通过函数 lm() 进行线性回归。
lm() 函数用于创建自变量与因变量之间的关系模型。
lm() 函数语法格式如下:
lm(formula,data)
参数说明:
- formula - 一个符号公式,表示 x 和 y 之间的关系。
- data - 应用数据。
创建关系模型,并获取系数:
实例
# 样本数据
x <- c(151, 174, 138, 186, 128, 136, 179, 163, 152, 131)
y <- c(63, 81, 56, 91, 47, 57, 76, 72, 62, 48)
# 提交给 lm() 函数
relation <- lm(y~x)
print(relation)
x <- c(151, 174, 138, 186, 128, 136, 179, 163, 152, 131)
y <- c(63, 81, 56, 91, 47, 57, 76, 72, 62, 48)
# 提交给 lm() 函数
relation <- lm(y~x)
print(relation)
执行以上代码输出结果为:
Call:lm(formula = y ~ x)Coefficients:(Intercept) x -38.4551 0.6746
使用 summary() 函数获取关系模型的概要:
实例
x <- c(151, 174, 138, 186, 128, 136, 179, 163, 152, 131)
y <- c(63, 81, 56, 91, 47, 57, 76, 72, 62, 48)
# 提交给 lm() 函数
relation <- lm(y~x)
print(summary(relation))
y <- c(63, 81, 56, 91, 47, 57, 76, 72, 62, 48)
# 提交给 lm() 函数
relation <- lm(y~x)
print(summary(relation))
执行以上代码输出结果为:
Call:lm(formula = y ~ x)Residuals: Min 1Q Median 3Q Max -6.3002 -1.6629 0.0412 1.8944 3.9775 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -38.45509 8.04901 -4.778 0.00139 ** x 0.67461 0.05191 12.997 1.16e-06 ***---Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1Residual standard error: 3.253 on 8 degrees of freedomMultiple R-squared: 0.9548, Adjusted R-squared: 0.9491 F-statistic: 168.9 on 1 and 8 DF, p-value: 1.164e-06
predict() 函数
predict() 函数用于根据我们建立的模型来预测数值。
predict() 函数语法格式如下:
predict(object, newdata)
参数说明:
- object - lm() 函数创建的公式。
- newdata - 要预测的值。
以下实例我们预测一个新的体重值:
实例
# 样本数据
x <- c(151, 174, 138, 186, 128, 136, 179, 163, 152, 131)
y <- c(63, 81, 56, 91, 47, 57, 76, 72, 62, 48)
# 提交给 lm() 函数
relation <- lm(y~x)
# 判断身高为 170cm 的体重
a <- data.frame(x = 170)
result <- predict(relation,a)
print(result)
x <- c(151, 174, 138, 186, 128, 136, 179, 163, 152, 131)
y <- c(63, 81, 56, 91, 47, 57, 76, 72, 62, 48)
# 提交给 lm() 函数
relation <- lm(y~x)
# 判断身高为 170cm 的体重
a <- data.frame(x = 170)
result <- predict(relation,a)
print(result)
执行以上代码输出结果为:
1 76.22869
我们也可以生存一个图表:
实例
# 样本数据
x <- c(151, 174, 138, 186, 128, 136, 179, 163, 152, 131)
y <- c(63, 81, 56, 91, 47, 57, 76, 72, 62, 48)
relation <- lm(y~x)
# 生存 png 图片
png(file = "linearregression.png")
# 生成图表
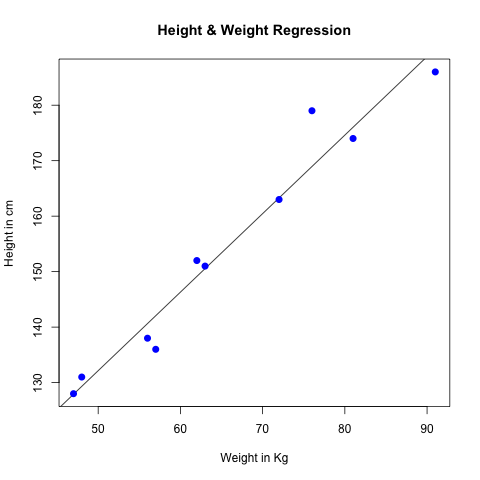
plot(y,x,col = "blue",main = "Height & Weight Regression",
abline(lm(x~y)),cex = 1.3,pch = 16,xlab = "Weight in Kg",ylab = "Height in cm")
x <- c(151, 174, 138, 186, 128, 136, 179, 163, 152, 131)
y <- c(63, 81, 56, 91, 47, 57, 76, 72, 62, 48)
relation <- lm(y~x)
# 生存 png 图片
png(file = "linearregression.png")
# 生成图表
plot(y,x,col = "blue",main = "Height & Weight Regression",
abline(lm(x~y)),cex = 1.3,pch = 16,xlab = "Weight in Kg",ylab = "Height in cm")
图表如下:

 R 语言实例
R 语言实例