加载规划求解加载项 | 制定模型 | 反复试验 | 解决模型
Excel包括一个称为“ 求解器”的工具,该工具使用运筹学中的技术来查找各种决策问题的最佳解决方案。
加载规划求解加载项
要加载求解器加载项,请执行以下步骤。
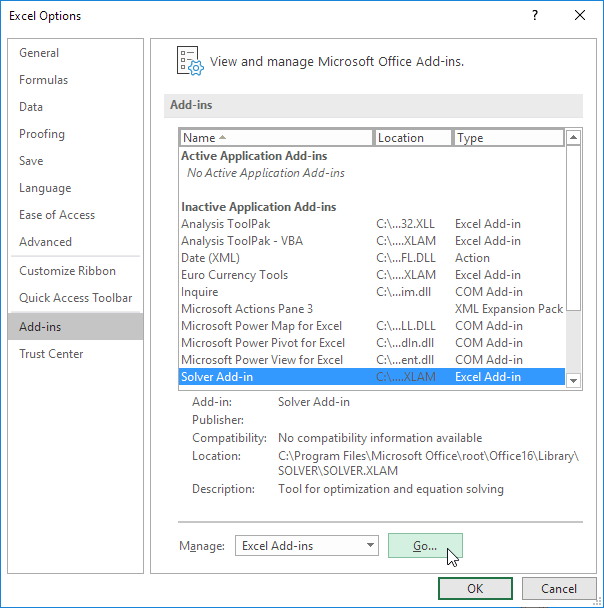
1.在文件选项卡上,单击选项。
2.在“加载项”下,选择“求解器加载项”,然后单击“执行”按钮。
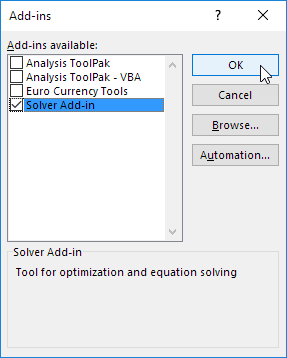
3.检查规划求解加载项,然后单击确定。
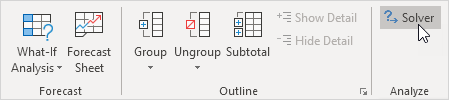
4.您可以在“数据”选项卡上的“分析”组中找到“求解器”。
制定模型
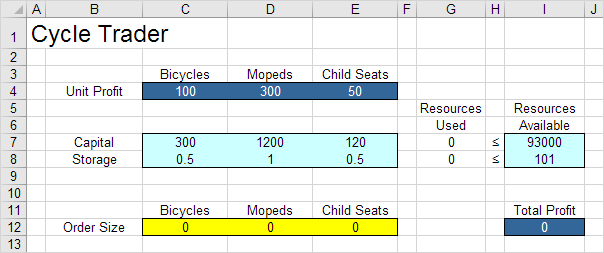
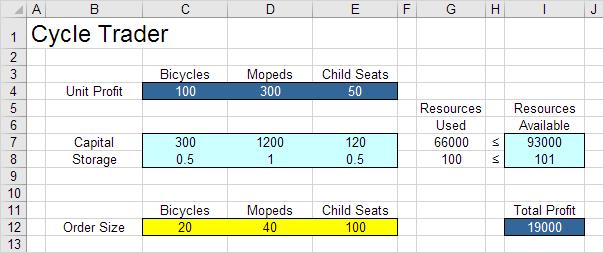
我们要解决的模型在Excel中如下所示。
1.要制定此线性规划模型,请回答以下三个问题。
一个。要做出什么决定?对于此问题,我们需要Excel找出每种产品(自行车,轻便摩托车和儿童座椅)的订购量。
b。这些决定受到哪些限制?这里的约束是产品使用的资本和存储量不能超过可用资本和存储(资源)的有限数量。例如,每辆自行车使用300单位的资本和0.5单位的存储空间。
C。这些决策的总体绩效指标是什么?绩效的总体衡量标准是这三种产品的总利润,因此目标是使该数量最大化。
2.为了使模型更易于理解,请命名以下范围。
| 范围名称 | 细胞 |
|---|---|
| 单位利润 | C4:E4 |
| 订单大小 | C12:E12 |
| 使用资源 | G7:G8 |
| 可用资源 | I7:I8 |
| 全面利润 | I12 |
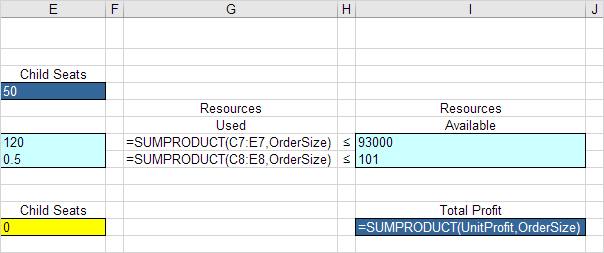
3.插入以下三个SUMPRODUCT函数。
说明:资本的使用量等于SUMPRODUCT范围C7的:E7和OrderSize。使用的存储量等于范围C8:E8和OrderSize的总和。总利润等于UnitProfit和OrderSize的总和。
试错
使用这种公式,可以轻松分析任何试验解决方案。
例如,如果我们订购20辆自行车,40辆轻便摩托车和100个儿童座椅,则所使用的资源总量不会超过可用资源的总量。该解决方案的总利润为19000。
不必使用反复试验。接下来,我们将描述如何使用Excel Solver快速找到最佳解决方案。
解决模型
要找到最佳解决方案,请执行以下步骤。
1.在“数据”选项卡上的“分析”组中,单击“ 求解器”。
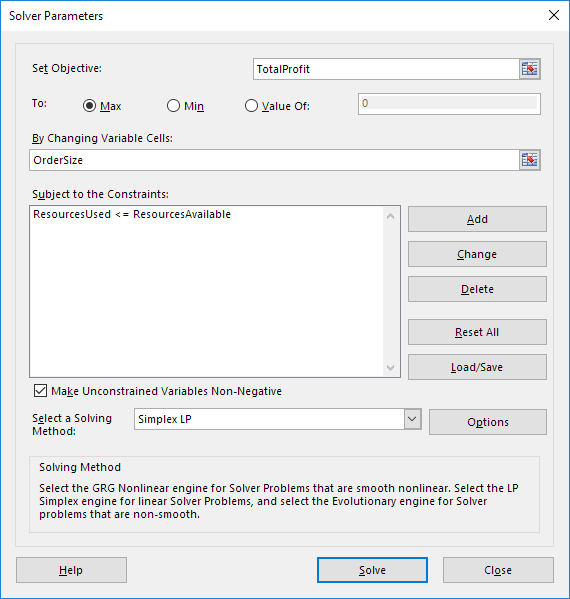
输入求解器参数(继续)。结果应与下图一致。
您可以选择键入范围名称或单击电子表格中的单元格。
2.为目标输入TotalProfit。
3.单击最大。
4.为更改的变量单元格输入OrderSize。
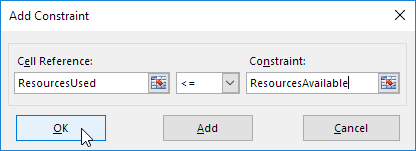
5.单击添加输入以下约束。
6.选中“使非约束变量为负”,然后选择“ Simplex LP”。
7.最后,单击解决。
结果:
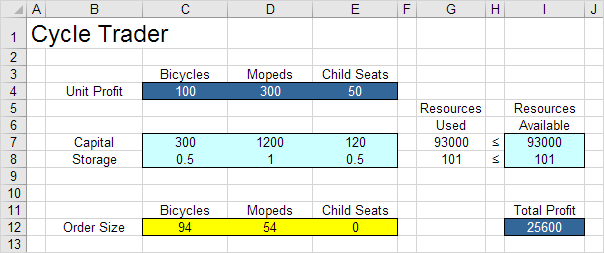
最佳解决方案:
结论:订购94辆自行车和54辆轻便摩托车最好。该解决方案的最大利润为25600。该解决方案使用了所有可用资源。