某个数学系列的第k 个项T k由以下公式定义:
| Ť ķ | = | k 2 + 6k + 1 |
| 9k + 7 |
通过将k = 1代入公式即可获得该系列的第一项T 1,即
| Ť 1 | = | 1 2 + 6 + 1 | = | 1个 | 和 |
| 9 + 7 | 2 |
| Ť 2 | = | 2 2 + 12 + 1 | = | 17 | ... 等等 |
| 18 + 7 | 25 |
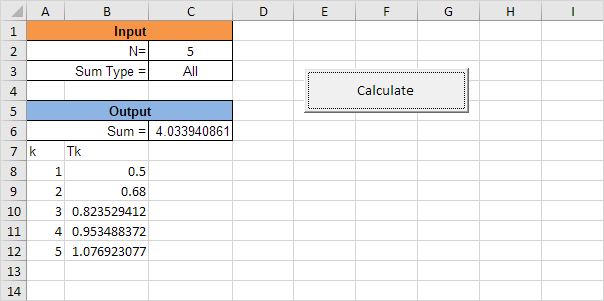
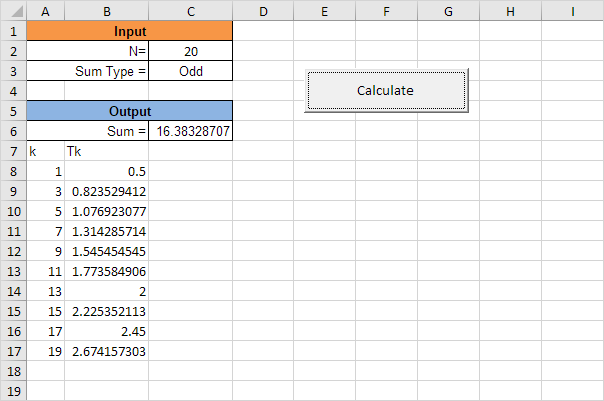
下面我们将看一下Excel VBA中的程序,该程序可计算任何项T k以及不超过N的项之和。
说明:用户可以选择输入“全部”或“奇数”,以分别计算该系列的前N个项的和或仅计算不超过N个奇数项的和。
在您的工作表上放置一个命令按钮,并添加以下代码行:
1.首先,我们声明四个Integer类型的变量和一个String类型的变量。
Dim i,term,N,stepSize 作为 整数
Dim sumType 作为 字符串
Dim sumType 作为 字符串
2.第二,我们初始化变量。
i = 0
N = Range(“ C2”)。Value
sumType = Range(“ C3”)。Value
N = Range(“ C2”)。Value
sumType = Range(“ C3”)。Value
3.清空字段。
Range(“ A8:B1000”)。Value =“”
Range(“ C6”)。Value =“”
Range(“ C6”)。Value =“”
4.确定stepSize。
选择 Case sumType
Case Is =“ All”
stepSize = 1
Case Is =“ Odd”
stepSize = 2
Case Else
MsgBox“在单元格C3中输入有效表达式”
结束
结束 选择
Case Is =“ All”
stepSize = 1
Case Is =“ Odd”
stepSize = 2
Case Else
MsgBox“在单元格C3中输入有效表达式”
结束
结束 选择
提示:浏览我们的Select Case程序以了解有关Select Case结构的更多信息。
5.进行计算。
对于条件= 1 至 N 步 stepSize
单元格(8 + i,1)。值=项
Cells(8 + i,2)。值=(条件^ 2 +(6 *项)+1)/(((9 *项) )+ 7)
Range(“ C6”)。Value = Range(“ C6”)。Value + Cells(8 + i,2).Value
i = i + 1
下一项
单元格(8 + i,1)。值=项
Cells(8 + i,2)。值=(条件^ 2 +(6 *项)+1)/(((9 *项) )+ 7)
Range(“ C6”)。Value = Range(“ C6”)。Value + Cells(8 + i,2).Value
i = i + 1
下一项
说明:我们使用Step关键字为循环的counter变量指定增量(“ All”为1,“ Odd”为2)。
结果: