autocorrelation即自相关性,又被称为序列相关性,字头auto来自于希腊语,意思是“自己的,本身的”。自相关性是指按照发生的时间先后顺序排列而成的一个数据系列与其自身而不是其他数据产生了相关关系,体现的是该系列数据受自身历史演变过程的影响程度。
在资产价格走势分析方面,分析师可根据资产价格的自相关性分析以往的价格走势会对未来的价格变动产生多大的影响。以股票为例,假设一只股票在以往的行情中展现出很高的自相关性,同时该股票的价格一直在上涨,那么就有理由认为过去一段时间的上升动能会得以延续,股价未来还会继续上涨。
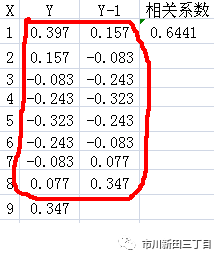
以下表为例,表中Y列共有9个数据,如果将第一个数据0.397去掉,整列数据就会上移一格,在Y-1列显示的就是其余8个数据,如果去掉Y列最后一个数据,计算剩余8个数据与Y-1列的8个数据之间的相关系数,结果为0.6441,这就说明Y列数据在自身之间具有一定的相关性。
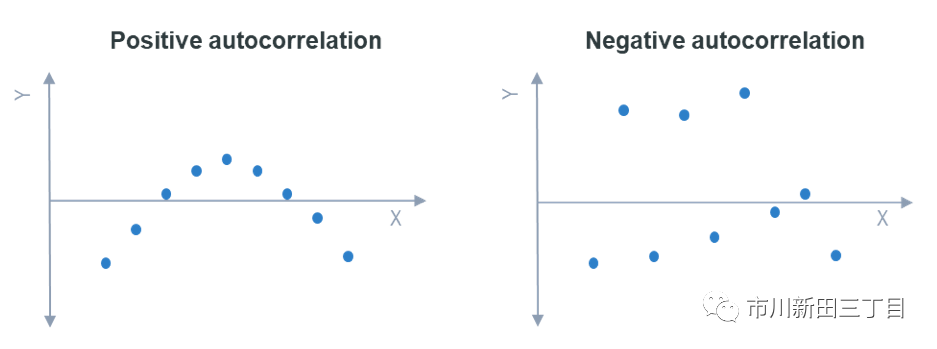
上例体现的是正的一阶自相关性,一阶是指该数据系列的当前值与自身前一个数值之间的相关性。如果一阶自相关系数是正的,相关图就会呈现出下面左图中光滑的蛇形形态;如果一阶自相关系数是负的,相关图就会呈现出下面右图中的之字形态。
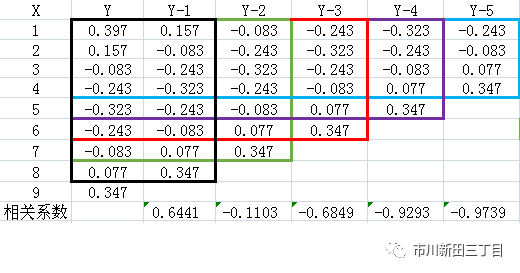
还是上面的例子,如果继续将第二、第三、第四、第五个数据去掉,就会得到以下自相关系数的计算结果
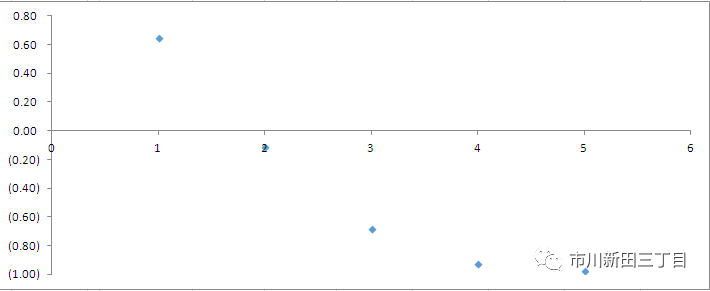
将自相关系数的数值做成相关图,显示如下:
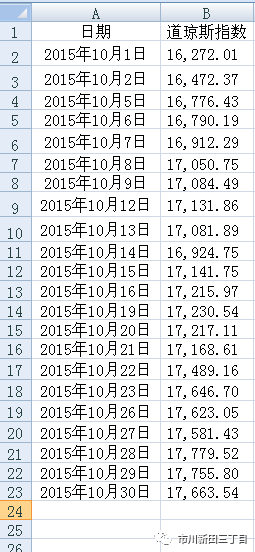
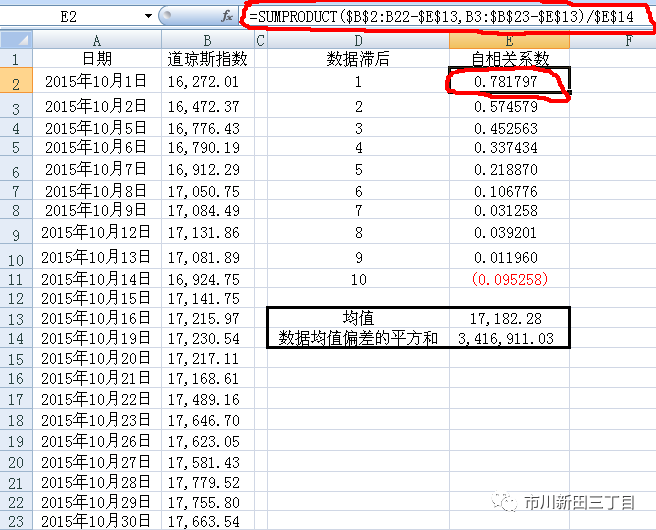
本文的主题是如何用EXCEL计算自相关系数。以道琼斯指数2015年10月份的收盘点位为例,
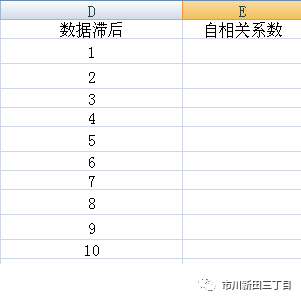
设定10个数据滞后期
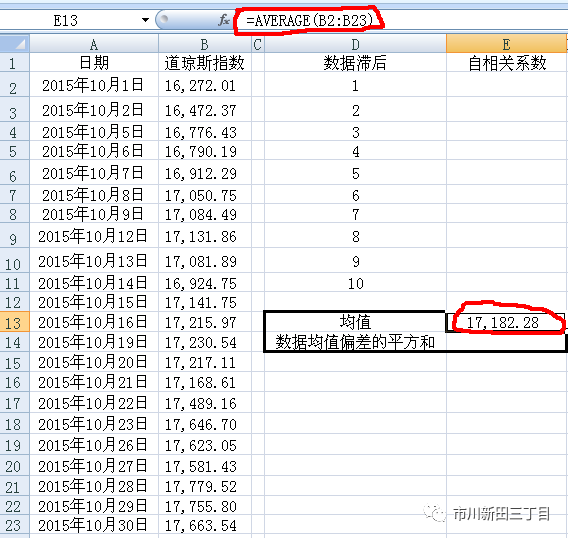
计算10月份道琼斯指数收盘点位的均值,结果为17182.28
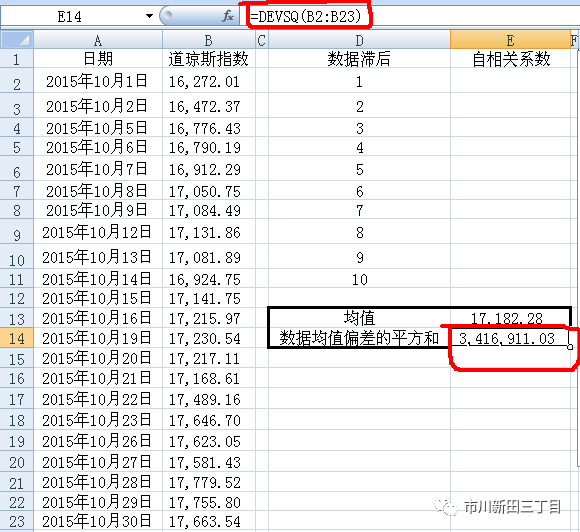
用DEVSQ()函数计算道琼斯指数每日收盘点位与均值17182.28的差值的平方之和
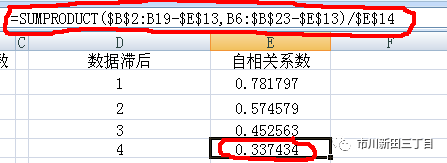
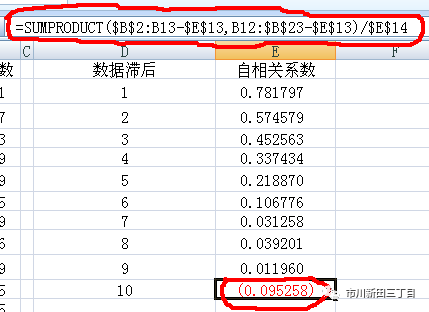
根据以下公式计算自相关系数
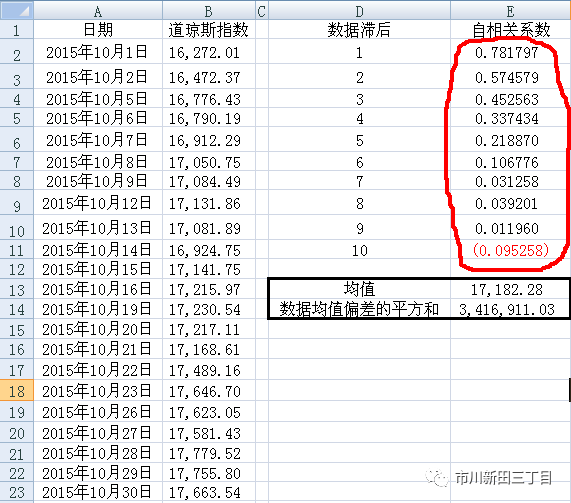
所有结果计算显示如下,可以看到自相关系数从高到低,逐渐接近零,为自相关系数比较典型的排列情况。